LoRa, QLoRA and QA-LoRA: Efficient Adaptability in Large Language Models Through Low-Rank Matrix Factorization

Large Language Models (LLMs) have carved a unique niche, offering unparalleled capabilities in understanding and generating human-like text. The power of LLMs can be traced back to their enormous size, often having billions of parameters. While this huge scale fuels their performance, it simultaneously births challenges, especially when it comes to model adaptation for specific tasks or domains. The conventional pathways of managing LLMs, such as fine-tuning all parameters, present a heavy computational and financial toll, thus posing a significant barrier to their widespread adoption in real-world applications.

In a previous article, we delved into fine-tuning Large Language Models (LLMs) to tailor them to specific requirements. We explored various fine-tuning methodologies such as Instruction-Based Fine-Tuning, Single-Task Fine-Tuning, and Parameter Efficient Fine-Tuning (PEFT), each with its unique approach towards optimizing LLMs for distinct tasks. Central to the discussion was the transformer architecture, the backbone of LLMs, and the challenges posed by the computational and memory demands of handling a vast number of parameters during fine-tuning.

The above image represents the scale of various large language models, sorted by their number of parameters. Notably: PaLM, BLOOM, etc.

As of this year, there have been advancements leading to even way larger models. However, tuning such gigantic, open-source models on standard systems is unfeasible without specialized optimization techniques.

Enter Low-Rank Adaptation (LoRA) was introduced by Microsoft in this paper, aiming to mitigate these challenges and render LLMs more accessible and adaptable.

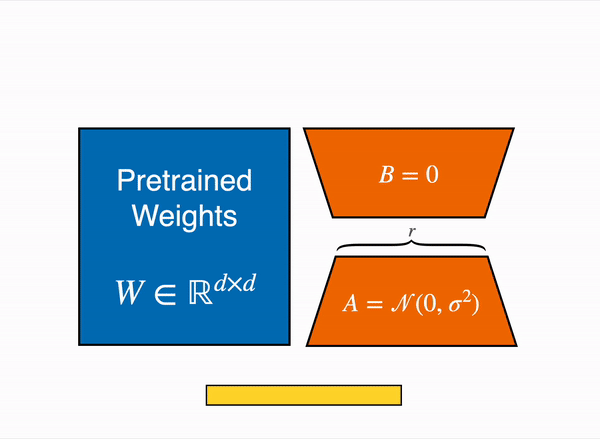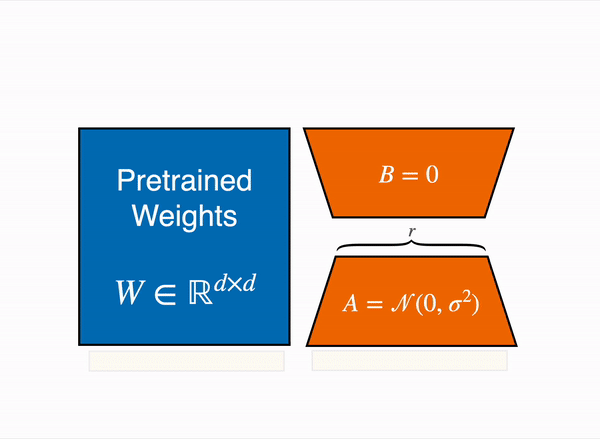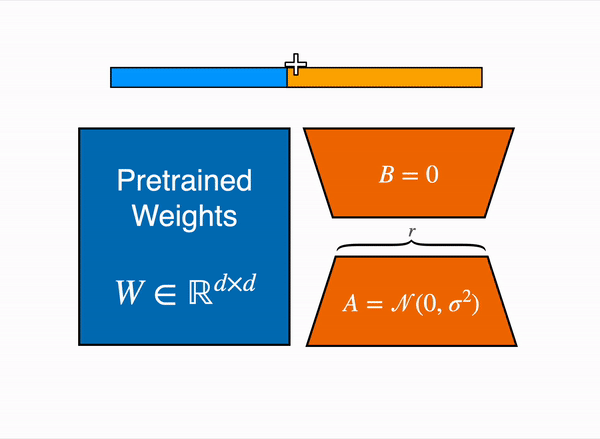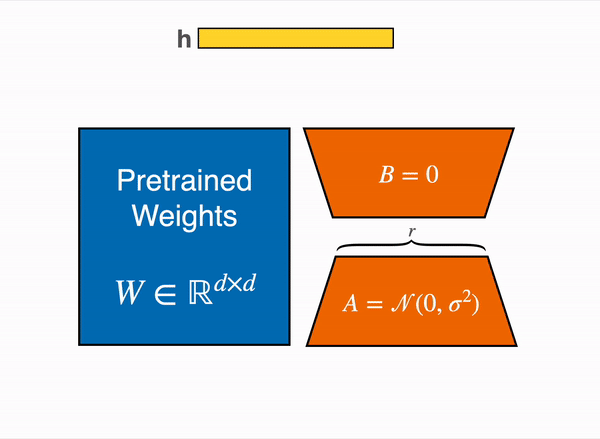
The crux of LoRA lies in its approach towards model adaptation without delving into the intricacies of re-training the entire model. Unlike traditional fine-tuning, where every parameter is subject to change, LoRA adopts a smarter route. It freezes the pre-trained model weights and introduces trainable rank decomposition matrices into each layer of the Transformer architecture. This approach drastically trims down the number of trainable parameters, ensuring a more efficient adaptation process.

The Evolution of LLM tuning Strategies

Reflecting upon the journey of LLM tuning, one can identify several strategies employed by practitioners over the years. Initially, the spotlight was on fine-tuning the pre-trained models, a strategy that entails a comprehensive alteration of model parameters to suit the specific task at hand. However, as the models grew in size and complexity, so did the computational demands of this approach.

The next strategy that gained traction was subset fine-tuning, a more restrained version of its predecessor. Here, only a subset of the model’s parameters is fine-tuned, reducing the computational burden to some extent. Despite its merits, subset fine-tuning still was not able to keep up with the rate of growth in size of LLMs.

As practitioners ventured to explore more efficient avenues, full fine-tuning emerged as a rigorous yet rewarding approach.

Introduction to LoRA

The rank of a matrix gives us a glimpse into the dimensions created by its columns, being determined by the number of unique rows or columns it has.

• Full-Rank Matrix: Its rank matches the lesser number between its rows or columns.
• Low-Rank Matrix: With a rank notably smaller than both its row and column count, it captures fewer features.

Now, big models grasp a broad understanding of their domain, like language in language models. But, fine-tuning them for specific tasks often only needs highlighting a small part of these understandings. Here’s where LoRA shines. It suggests that the matrix showcasing these weight adjustments can be a low-rank one, thus capturing fewer features.

LoRA smartly limits the rank of this update matrix by splitting it into two smaller rank matrices. So instead of altering the whole weight matrix, it changes just a part of it, making the fine-tuning task more efficient.

Applying LoRA to Transformers

LoRA helps minimize the training load in neural networks by focusing on specific weight matrices. Under Transformer architecture, certain weight matrices are linked with the self-attention mechanism, namely Wq, Wk, Wv, and Wo, besides two more in the Multi-Layer Perceptron (MLP) module.

Transformers Architecture

 

Transformer Attention Heads

Mathematical Explanation behing LoRA

Let’s break down the maths behind LoRA:

1. Pre-trained Weight Matrix W0​:
   • It starts with a pre-trained weight matrix W0​ of dimensions $d\times k$. This means the matrix has $d$ rows and $k$ columns.
2. Low-rank Decomposition:
   • Instead of directly updating the entire matrix W0​, which can be computationally expensive, the method proposes a low-rank decomposition approach.
   • The update $\Delta W$ to W0​ can be represented as a product of two matrices: $B$ and $A$.
     • $B$ has dimensions $d\times r$
     • $A$ has dimensions $r\times k$
   • The key point here is that the rank $r$ is much smaller than both $d$ and $k$, which allows for a more computationally efficient representation.
3. Training:
   • During the training process, W0​ remains unchanged. This is referred to as “freezing” the weights.
   • On the other hand, $A$ and $B$ are the trainable parameters. This means that, during training, adjustments are made to the matrices $A$ and $B$ to improve the model’s performance.
4. Multiplication and Addition:
   • Both W0​ and the update $\Delta W$ (which is the product of $B$ and $A$) are multiplied by the same input (denoted as $x$).
   • The outputs of these multiplications are then added together.
   • This process is summarized in the equation: h=W0​x+ΔWx=W0​x+BAx. Here, $h$ represents the final output after applying the updates to the input $x$.

In short, this method allows for a more efficient way to update a large weight matrix by representing the updates using a low-rank decomposition, which can be beneficial in terms of computational efficiency and memory usage.

LORA

Initialization and Scaling:

When training models, how we initialize the parameters can significantly affect the efficiency and effectiveness of the learning process. In the context of our weight matrix update using $A$ and $B$:

1. Initialization of Matrices $A$ and $B$:
   • Matrix $A$: This matrix is initialized with random Gaussian values, also known as a normal distribution. The rationale behind using Gaussian initialization is to break the symmetry: different neurons in the same layer will learn different features when they have different initial weights.
   • Matrix $B$: This matrix is initialized with zeros. By doing this, the update $\Delta W=BA$ starts as zero at the beginning of training. It ensures that there’s no abrupt change in the model’s behavior at the start, allowing the model to gradually adapt as $B$ learns appropriate values during training.
2. Scaling the Output from $\Delta W$:
   • After computing the update $\Delta W$, its output is scaled by a factor of rα​ where $\alpha$ is a constant. By scaling, the magnitude of the updates is controlled.
   • The scaling is especially crucial when the rank $r$ changes. For instance, if you decide to increase the rank for more accuracy (at the cost of computation), the scaling ensures that you don’t need to adjust many other hyperparameters in the process. It provides a level of stability to the model.

LoRA’s Practical Impact

LoRA has demonstrated its potential to tune LLMs to specific artistic styles efficiently by peoplr from AI community. This was notably showcased in the adaptation of a model to mimic the artistic style of Greg Rutkowski.

As highlighed in the paper with GPT-3 175B as an example. Having individual instances of fine-tuned models with 175B parameters each is quite costly. But, with LoRA, the trainable parameters drop by 10,000 times, and GPU memory usage is trimmed down to a third.

LoRa impact on GPT-3 Fine Tuning

The LoRA methodology not only embodies a significant stride towards making LLMs more accessible but also underscores the potential to bridge the gap between theoretical advancements and practical applications in the AI domain. By alleviating the computational hurdles and fostering a more efficient model adaptation process, LoRA is poised to play a pivotal role in the broader adoption and deployment of LLMs in real-world scenarios.

QLoRA (Quantized)

While LoRA is a game-changer in reducing storage needs, it still demands a hefty GPU to load the model for training. Here’s where QLoRA, or Quantized LoRA, steps in, blending LoRA with Quantization for a smarter approach.

Quantization

Normally, weight parameters are stored in a 32-bit format (FP32), meaning each element in the matrix takes up 32 bits of space. Imagine if we could squeeze the same info into just 8 or even 4 bits. That’s the core idea behind QLoRA. Quantization referes to the process of mapping continuous infinite values to a smaller set of discrete finite values. In the context of LLMs, it refers to the process of converting the weights of the model from higher precision data types to lower-precision ones.

Quantization in LLM

Here’s a simpler breakdown of QLoRA:

1. Initial Quantization: First, the Large Language Model (LLM) is quantized down to 4 bits, significantly reducing the memory footprint.
2. LoRA Training: Then, LoRA training is performed, but in the standard 32-bit precision (FP32).

Now, you might wonder, why go back to 32 bits for training after shrinking down to 4 bits? Well, to effectively train LoRA adapters in FP32, the model weights need to revert to FP32 too. This switch back and forth is done in a smart, step-by-step manner to avoid overwhelming the GPU memory.

LoRA finds its practical application in the Hugging Face Parameter Efficient Fine-Tuning (PEFT) library, simplifying its utilization. For those looking to use QLoRA, it’s accessible through a combination of the bitsandbytes and PEFT libraries. Additionally, the HuggingFace Transformer Reinforcement Learning (TRL) library facilitates supervised fine-tuning with an integrated support for LoRA. Together, these three libraries furnish the essential toolkit for fine-tuning a selected pre-trained model, enabling the generation of persuasive and coherent product descriptions when prompted with specific attribute instructions.

Post fine-tuning from QLoRA, the weights has to revert back to a high-precision format, which can lead to accuracy loss and lacks optimization for speeding up the process.

A proposed solution is to group the weight matrix into smaller segments and apply quantization and low-rank adaptation to each group individually. A new method, named QA-LoRA, tries to blend the benefits of quantization and low-rank adaptation while keeping the process efficient and the model effective for the desired tasks.

Conclusion

In this article we touched on the challenges posed by their enormous parameter size. We delved into traditional fine-tuning practices and their associated computational and financial demands. The crux of LoRA lies in its capability to modify pre-trained models without retraining them entirely, thereby reducing the trainable parameters and making the adaptation process more cost-effective.

We also delved briefly into Quantized LoRA (QLoRA), a  blend of LoRA and Quantization which reduces the memory footprint of the model while retaining the essential precision for training. With these advanced techniques, practitioners are now equipped with a robust libraries, facilitating the easier adoption and deployment of LLMs across a spectrum of real-world scenarios.

Matrix

These strategies are crafted to balance between making LLMs adaptable for specific tasks and ensuring the fine-tuning and deployment processes are not overly demanding in terms of computation and storage resources.